Recently, the Doubao (Seed) team introduced BFS-Prover, an efficient automated formal theorem proving system based on large language models (LLMs) and best-first search (BFS).

The team found that the simple BFS method, after systematic optimization, can deliver superior performance and efficiency in large-scale theorem-proving tasks without the need for complex Monte Carlo tree search or value functions.

BFS-Prover achieved a 72.95% accuracy on the benchmark MiniF2F test set of mathematical theorem proving, surpassing all previous approaches.

Automated formal mathematical theorem proving is an important AI application in the field of mathematical reasoning. Such tasks require the translation of mathematical propositions and proof steps into computer-verifiable code, which not only ensures the rigor of the reasoning process, but also builds a reusable mathematical knowledge base that provides a solid foundation for scientific research.

As early as the mid-20th century, many logicians, mathematicians, and AI pioneers such as Davis, Minsky, and Wang Hao have explored related issues.

In recent years, with the help of LLMs, automated theorem provers rely more on the complex Monte Carlo tree search (MCTS) or value functions to guide the search process.

However, these approaches introduce additional computational costs and system complexity, limiting the scalability of models in large-scale reasoning tasks.

The BFS-Prover from the ByteDance Doubao (Seed) team challenges this paradigm.

As a simpler, lighter, but highly competitive automatic theorem prover, it introduces three key technologies: Expert Iteration with adaptive data filtering, direct preference optimization (DPO) from Lean4 compiler feedback, and length normalization in BFS.

Results showed that BFS-Prover achieved a 72.95% accuracy on the formal mathematics test set MiniF2F, setting a new field record.

This result also proves for the first time that, with a sound optimization strategy, a simple BFS method can outperform mainstream sophisticated search algorithms such as MCTS and value functions.

The paper is now publicly available, and the model has been open sourced. We look forward to further communication with relevant researchers.

BFS-Prover: Scalable Best-First Tree Search for LLM-based Automatic Theorem Proving

Link to study: https://arxiv.org/abs/2502.03438

Link to HuggingFace: https://huggingface.co/bytedance-research/BFS-Prover

1. Are Mainstream Methods like MCTS and Value Functions Necessary?

In the field of formal mathematical proving, translating abstract mathematical concepts into rigorous forms that can be verified by computers is a challenging task.

The process requires that every step of reasoning follows strict formal logic rules, and that every step must be verified by the Lean proof assistant.

In the automated formal theorem-proving process, the core challenge for computers is to find valid paths in large and highly structured proof spaces. This difficulty is fundamentally different from traditional search problems, as shown below:

1) Large search spaces: Each step of reasoning may involve dozens or even hundreds of possible strategic choices;

2) Dynamic strategic space: Unlike the fixed rules of chess games, the set of applicable strategies in mathematical theorem proving is constantly changing, large in scale, and without clear boundaries;

3) Sparse and delayed feedback: It is difficult for the system to get effective intermediate feedback until the proof is completed;

4) Open-ended reasoning process: The lack of clear end states allows a proof attempt to theoretically continue indefinitely;

Automated theorem provers such as DeepSeek-Prover-V1.5 and InternLM2.5-StepProver primarily rely on complex MCTS and value functions to solve the above problems.

These AlphaZero-like algorithms have excelled in games, especially Go, and made reinforcement learning a widely known concept. However, these mainstream methods underperform in the field of automated theorem proving due to the complexity of state spaces and the lack of clear process reward signals. In addition, complex search algorithms have resulted in high computational costs and increased system complexity.

2. Simplifying the Complex: Proving Mathematical Theorems with Machines Can be Simpler

Humans often prioritize the most likely solution after encountering problems. The best-first tree search (BFS) works similarly.

This is an algorithm that searches for nodes in a "tree" or "graph." Its core idea is to evaluate each node's priority based on some heuristic function and access nodes by priority. It is often used to solve constraint-satisfaction problems and combinatorial optimization problems, especially when near-optimal solutions need to be found quickly.

Previously, many researchers believed that simple BFS algorithms lacked an effective exploration mechanism, especially the exploration of deep paths, making it unsuitable for large-scale theorem-proving tasks. However, researchers from the Doubao (Seed) team found a breakthrough and proposed the BFS-Prover system.

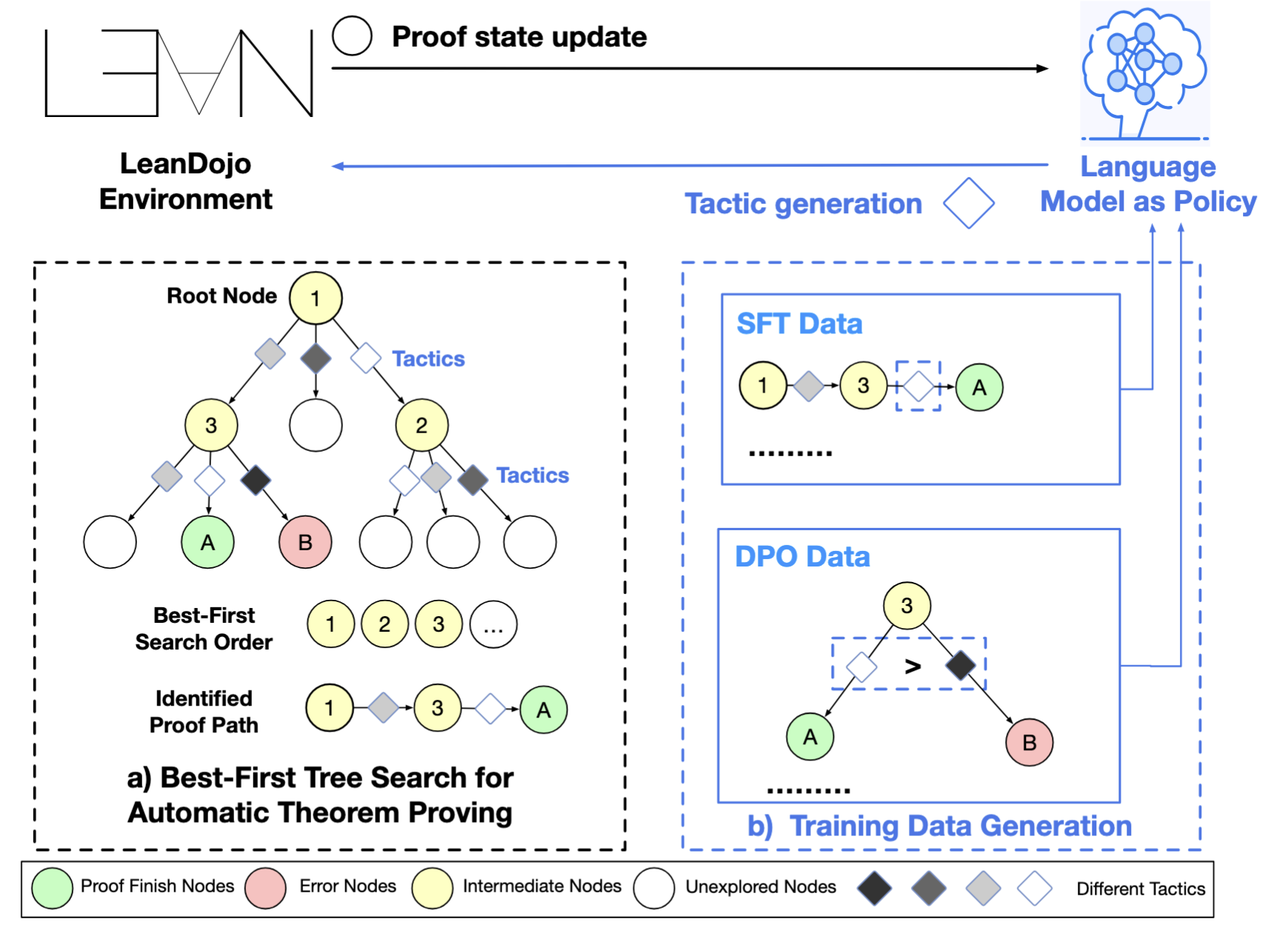
The figure below illustrates the overall architecture and workflow of the BFS-Prover system.

Right side: The generation process of training data, including SFT data for supervised fine-tuning (state-tactic pairs along successful proof paths) and DPO data for direct preference optimization (correct vs. incorrect tactics from the same state).

Left side: The BFS mechanism interacting with Lean4 via the LeanDojo environment. Starting with the root node, it explores proof paths in priority order (1→2→3...) until the proof completion node (green A) is found.

The whole system forms a closed loop: LLM Generation Strategy → LeanDojo Execution → Get Feedback → Generate Training Data → Optimize LLM → Generate Strategy again, enabling an expert iteration mechanism for continuous improvement.

The team believes that the BFS-Prover system not only proves that optimized BFS methods outperform complex MCTS and value functions, but also maintains the simplicity and computational efficiency of the architecture. Its technical features are as follows:

Enabling the model to both think deeply about strategies and master the simplest proof methods

BFS-Prover uses an expert iteration framework to continuously enhance the LLM's capabilities through multiple iterations. In each round, the system first filters out solvable theorems using deterministic beam search, removes these "simple problems" from the training data, and then proceeds to solve "complex problems."

This innovative data filtering mechanism ensures that the training data increasingly emphasizes more challenging theorem proof tasks, allowing the LLM to learn more diverse proof strategies.

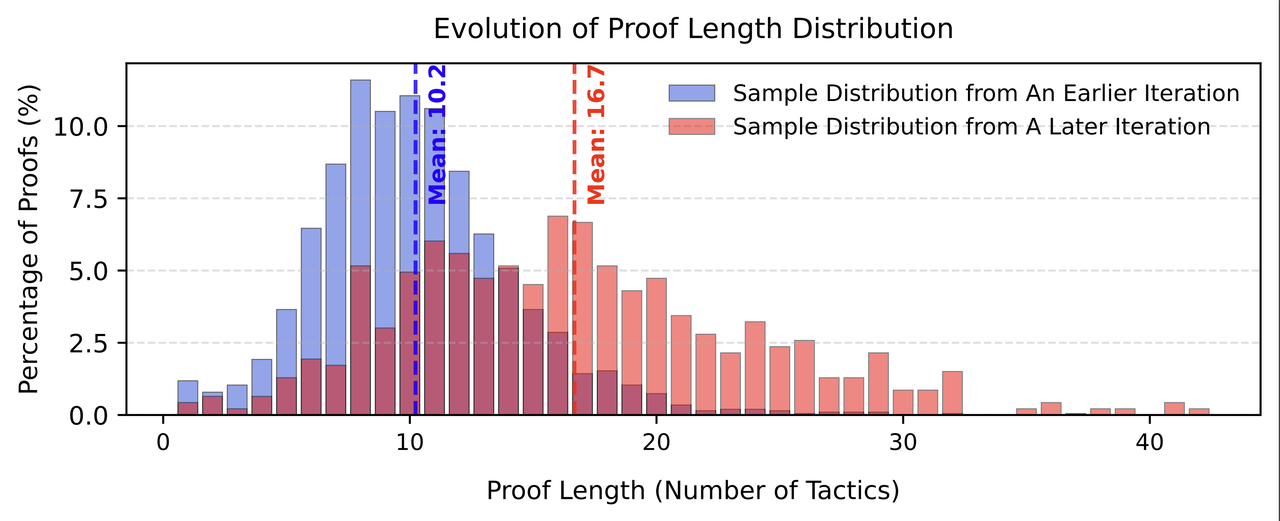
The experimental data shown in the figure below shows that as iterations proceed, the average proof length discovered by the system increases and the coverage increases, demonstrating the effectiveness of this approach.

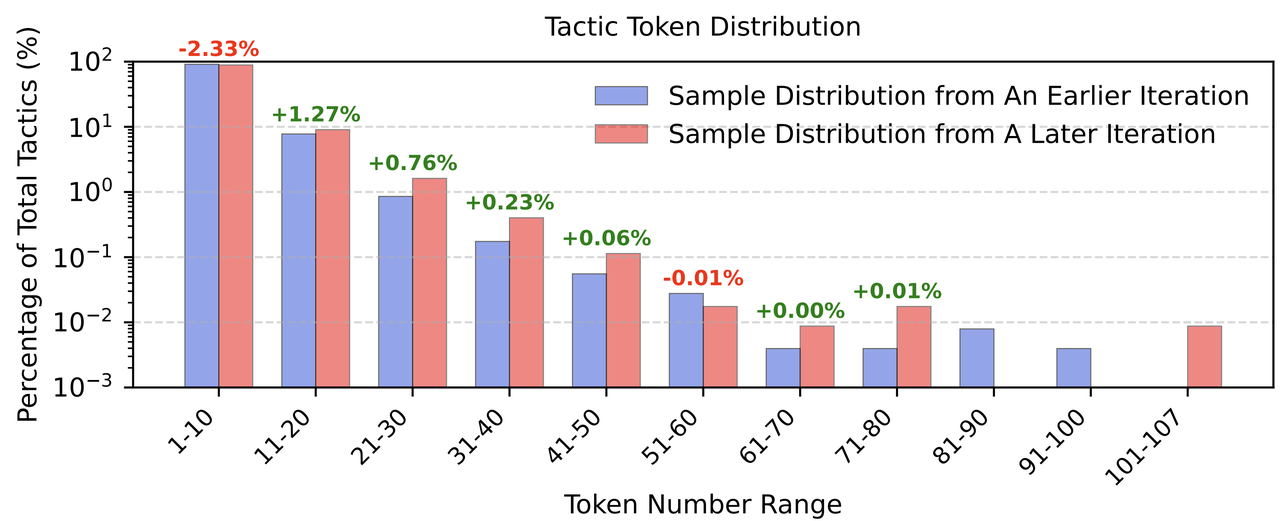
At the same time, the tactic distribution of LLM generation has evolved.

As shown in the figure below, the tactic length distribution generated by the model has changed significantly after multiple iterations: The ratio of very short tactics (1-10 tokens) decreased, while the ratio of medium-length tactics (11-50 tokens) increased.

This distributional shift suggests that LLM's "deep thinking ability" is increasing, avoiding the distributional collapse that often occurs in reinforcement learning, and gradually mastering more complex and informative proof strategies.

At the same time, the model has not lost its ability to generate concise tactics. Preserving this diversity in tactic generation is crucial for valid theorem proofs, because different proof states require tactics of different complexity, ranging from simple item rewrites to complex algebraic operations.

Summarizing "Proof Errors Steps" from the process to improve proof capabilities

During the proof search, when some of the tactics generated by the LLM cause a Lean4 compiler error, the system pairs these invalid tactics with the successful tactics to form a negative feedback signal.

BFS-Prover innovatively leverages this data to optimize the tactic LLM through direct preference optimization (DPO). This approach significantly improves the model's ability to identify effective tactics, optimizes the distribution of tactics, and improves the sampling efficiency of BFS.

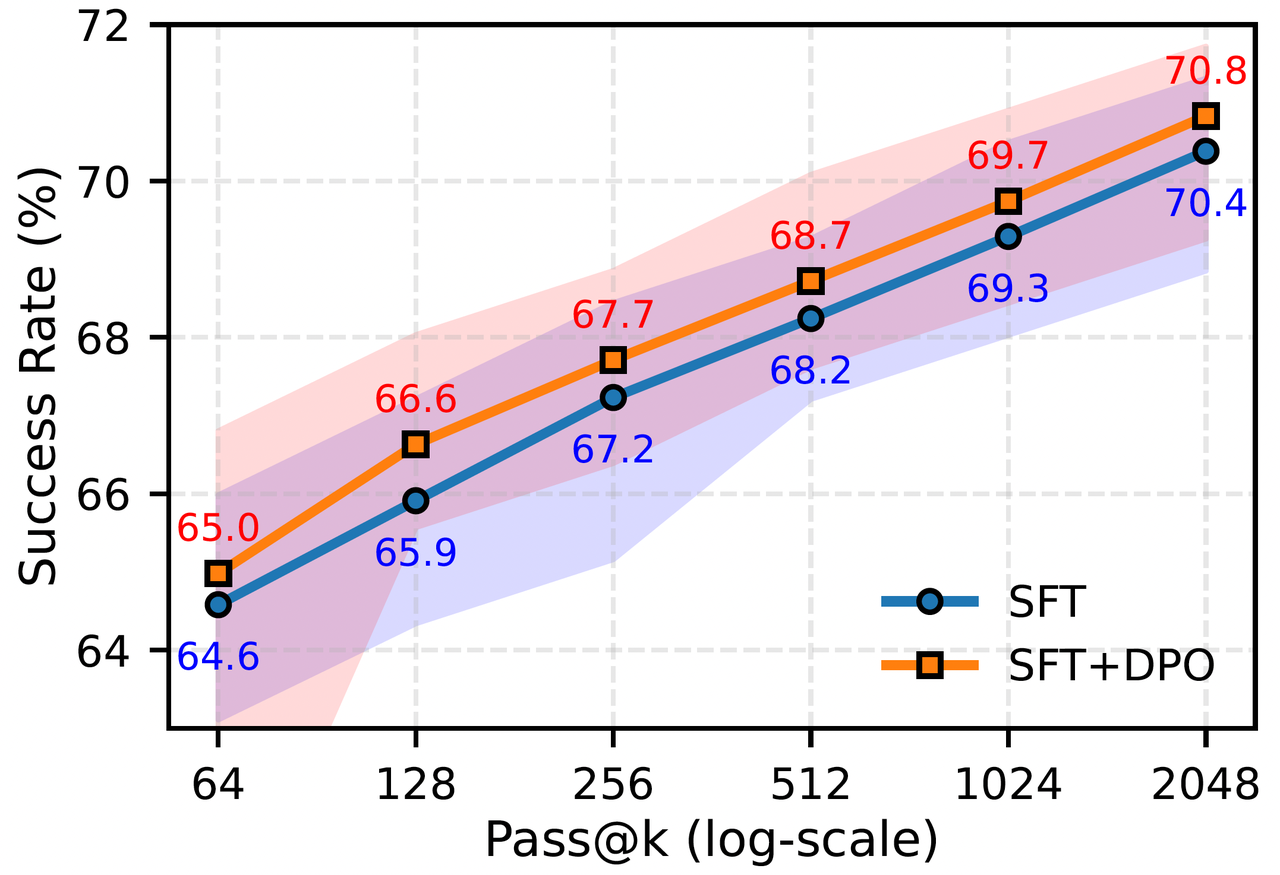
As shown in the experiment results below, the DPO-optimized model has achieved performance improvement at all computing scales, demonstrating the importance of negative signals in theorem proving.

Avoiding bias against deep reasoning and achieving breakthroughs in difficult theorem proofs

To mitigate BFS's inherent bias against deep reasoning paths, the BFS-Prover system introduces an adjustable length normalization scoring function:

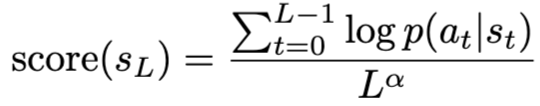
L represents the path length and α is the tunable length normalization parameter. By appropriately adjusting the value of α, the system can balance the exploitation of high-probability pathways with the exploration of deeper paths, enabling BFS to explore long-chain proofs more efficiently.

3. Achieving New SOTA on MiniF2F

The team conducted a comprehensive assessment of BFS-Prover on the MiniF2F test set. The test set is a recognized benchmark test set in formal mathematics, containing highly challenging, competition-level mathematics questions widely used to measure the capabilities of automated theorem provers.

Surpassing existing state-of-the-art systems

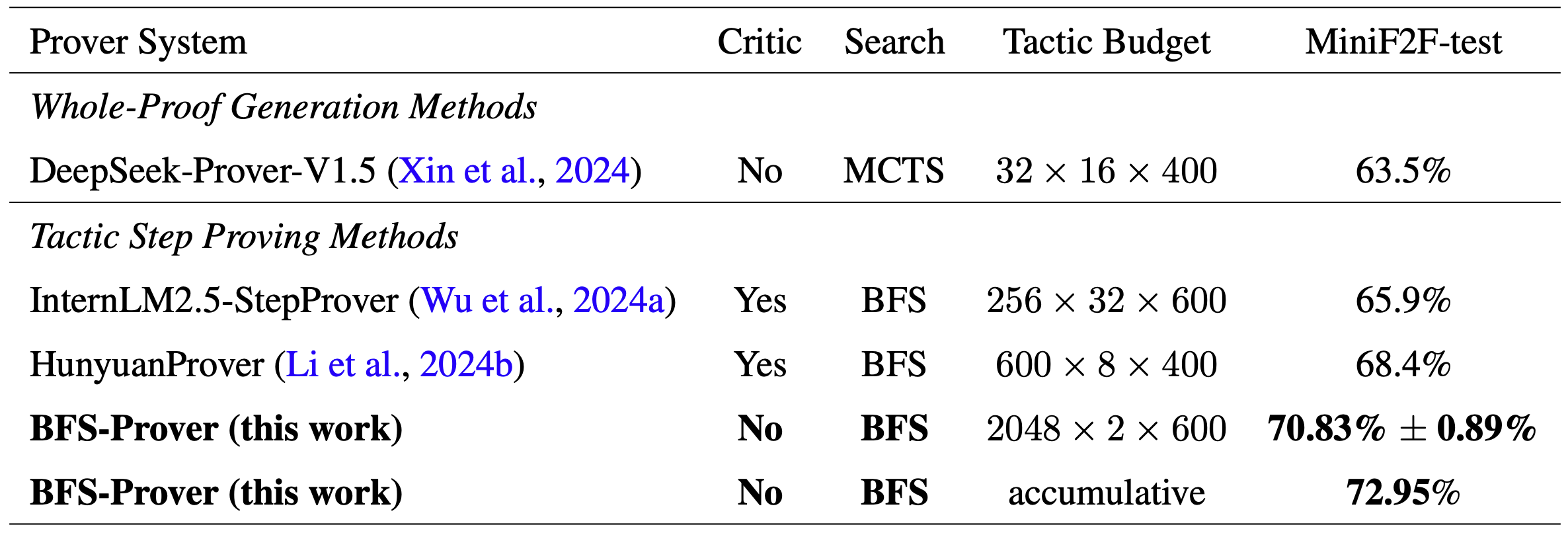
BFS-Prover shows significant advantages compared to previous theorem provers.

At a fixed tactic generation budget (2048 × 2 × 600 inference calls), BFS-Prover achieved a 70.83% accuracy, outperforming all existing systems, including InternLM2.5-StepProver (65.9%) using value functions, HunyuanProver (68.4%), and DeepSeek-Prover-V1.5 (63.5%) based on MCTS.

In the accumulative evaluation, BFS-Prover further improved the accuracy to 72.95%, becoming the new SOTA in the field of formal theorem proving.

This result not only demonstrates the potential of the BFS approach, but also shows how a simple algorithm can outperform a complex approach with careful design.

Successfully proving multiple IMO topics

It is worth mentioning that BFS-Prover successfully proved multiple IMO problems in MiniF2F-test, including imo_1959_p1, imo_1960_p2, imo_1962_p2, imo_1964_p2, and imo_1983_p6.

These proofs demonstrate the system's capability to handle complex mathematical reasoning, including number theory, inequality, and geometric relations.

For example, for the imo_1983_p6 inequality problem, BFS-Prover can generate a simple and elegant formal proof:

4. Final Thoughts

The team believes that the success of BFS-Prover carries an important insight into the field of automated theorem proving: Simple algorithms, combined with well-designed optimization strategies, can also help push the boundaries of AI4Math.

With the continuous improvement of the ability of large language models, the simple and efficient route pioneered by BFS-Prover is expected to further advance the development of automated formal theorem proving, providing more powerful automation tools for mathematical research.

Looking to the future, the team plans to further enhance the BFS method's ability to tackle more complex mathematical problems, particularly at the undergraduate- and graduate-level theorems. At the same time, the team will continue to tap the potential of models based on reasoning models and other cutting-edge methods.

We hope to accelerate the mathematical discovery process through continuous optimization of data and training strategies for tools that support mathematical research, ultimately realizing the vision of human-machine collaboration to solve cutting-edge mathematical challenges.

The Doubao (Seed) team remains committed to exploring the endless boundaries of intelligence and unlocking the infinite possibilities of general intelligence.