Peking University and ByteDance Launched FAN, an Improvement on Transformers, Focusing on Cyclical Features and Patterns
Peking University and ByteDance Launched FAN, an Improvement on Transformers, Focusing on Cyclical Features and Patterns
Date
2024-11-22
Category
Technology Launch
Recently, Peking University and the ByteDance Doubao (Seed) team announced FAN (Fourier Analysis Networks), a new type of neural network architecture.
By integrating Fourier analysis principles, FAN explicitly embeds periodic information into the network structure, allowing the models to more naturally capture and understand data's cyclical features. It can also seamlessly replace traditional MLP layers with fewer params and FLOPS.
Experiments showed that FAN performs significantly better than existing models not only in cyclical modeling, but also in practical tasks such as symbolic equation representation, time series forecasting, language modeling, and image recognition. For out-of-domain data, FAN also shows a clear advantage, proving its strong ability to extract and summarize periodic pattern features.
Currently, large transformer models are the mainstream, with typical examples including the GPT series, Llama series, and DiT models for image generation, among others.
However, when it comes to cyclical modeling, there are potential drawbacks with the classical transformer models integrated with MLPs. Even for the simple sine function, the existing transformer models are unable to fully understand its periodicity. During extrapolation, they go completely out of control and fail to effectively capture the essence of the cyclical phenomena.
The team of Professor Li Ge of Peking University and the ByteDance Doubao (Seed) team recently unveiled a new type of neural network architecture, FAN (Fourier Analysis Networks). By integrating Fourier analysis principles, FAN can embed periodic information directly into the network structure, allowing models to more naturally capture and understand cyclical features in data.
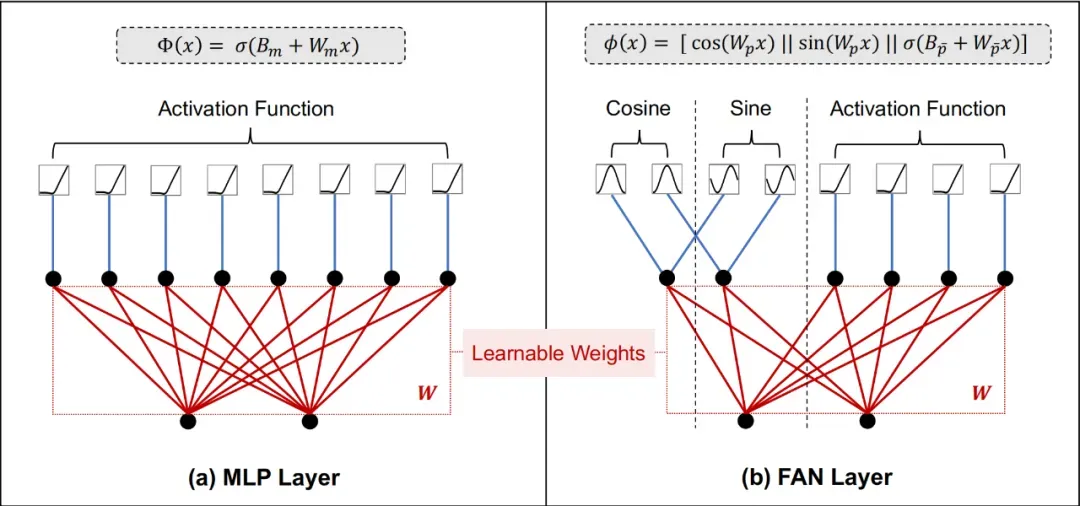
Note: Illustrations of MLP layer and FAN layer
Experiments showed that FAN not only performs significantly better than existing models in periodic modeling, but also outperforms mainstream models like transformers in practical tasks such as symbolic equation representation, time series forecasting, language modeling, and image recognition, especially on out-of-domain test data.
The team believes that FAN provides a new paradigm that can effectively model periodicity and seamlessly replace traditional MLPs while reducing the params and FLOPS, addressing the shortcomings in current foundation models on periodic modeling with vast application potential.

FAN: Fourier Analysis Networks
Link to study: https://arxiv.org/abs/2410.02675
Link to code: https://github.com/YihongDong/FAN
1. How the Fourier principle was integrated in Transformer
Cyclical phenomena are widespread and have a profound impact on human society and the natural sciences. As a key feature, periodicity is explicitly or implicitly present in numerous patterns, such as planetary motion in astronomy, seasonal changes in meteorology, circadian rhythms in biology, business cycles in economics, electromagnetic waves in physics, and mathematical algorithms and logical reasoning.
Good periodic modeling can improve the performance of the models in the above tasks. However, existing foundation models rely heavily on case-by-case data-driven optimization methods, and lack clear mechanisms to understand fundamental principles in data.
As a classical mathematical analytical tool, a Fourier series can dismantle a periodic function into a series of simple sine and cosine wave superpositions, which are widely used in signal processing, physics, and other fields. The team believed that, in theory, data containing complex cyclical features could also be broken down into simple sine and cosine representations.
Based on this idea, the joint research team of Peking University and Doubao (Seed) team hoped to build a simple neural network to model a Fourier series, as a substitute for MLPs.
In reality, however, the team faced a considerable theory-practice gap. It is already difficult to change a basic network architecture to keep its performance in line with MLPs on universal tasks, let alone add new cyclical modeling features for enhancement. In particular, the neural network is still a black box. As a result, the team found that while exploring its application, many theoretically feasible methods unexpectedly failed.
To this end, the team tried more than 60 modifications and finally found the most straightforward and efficient method, FAN.

Specifically, the team built a simple neural network tofS(x)f_S(x)fS(x)represent the expansion of a function into a Fourier series. We can express fS(x)f_S(x)fS(x)as follows:
fS(x)≜a0+∑n=1N(ancos(2πnxT)+bnsin(2πnxT)),=(I)a0+∑n=1N(wnccos(wninx)+wnssin(wninx)),=(II)B+[w1c,w2c,⋯ ,wnc]cos([w1in∣∣w2in∣∣⋯∣∣wnin]x)+[w1s,w2s,⋯ ,wns]sin([w1in∣∣w2in∣∣⋯∣∣wnin]x)=B+Wccos(Winx)+Wssin(Winx),=(III)B+Wout[cos(Winx)∣∣sin(Winx)],\begin{equation} \begin{aligned} f_{\text{S}}(x) & \triangleq a_0 + \sum_{n=1}^{N} \left( a_n \cos\left(\frac{2\pi nx}{T}\right) + b_n \sin\left(\frac{2\pi nx}{T}\right) \right), \\ & \mathop{=}\limits^{(\text{I})} a_0 + \sum_{n=1}^{N} \left( w^c_n \cos\left(w^\text{in}_nx\right) + w^s_n \sin\left(w^\text{in}_nx\right) \right), \\ & \mathop{=}\limits^{(\text{II})} B + [w^c_1, w^c_2, \cdots, w^c_n] \cos([w^\text{in}_1|| w^\text{in}_2|| \cdots|| w^\text{in}_n] x) \\ & \quad + [w^s_1, w^s_2, \cdots, w^s_n] \sin([w^\text{in}_1|| w^\text{in}_2|| \cdots|| w^\text{in}_n] x) \\ & = B + W_c \cos(W_\text{in}x) + W_s \sin(W_\text{in}x), \\ & \mathop{=}\limits^{(\text{III})} B + W_\text{out}[\cos(W_\text{in}x)|| \sin(W_\text{in}x)], \end{aligned} \end{equation}fS(x)≜a0+n=1∑N(ancos(T2πnx)+bnsin(T2πnx)),=(I)a0+n=1∑N(wnccos(wninx)+wnssin(wninx)),=(II)B+[w1c,w2c,⋯,wnc]cos([w1in∣∣w2in∣∣⋯∣∣wnin]x)+[w1s,w2s,⋯,wns]sin([w1in∣∣w2in∣∣⋯∣∣wnin]x)=B+Wccos(Winx)+Wssin(Winx),=(III)B+Wout[cos(Winx)∣∣sin(Winx)],
where B, WinW_{in}Win,WoutW_{out}Woutare learnable parameters, (I) is calculated through a definite integral based onana_nanand bnb_nbn, (II) and (III) are equivalent forms of matrix operations, and [・||・] and [・,・] represent connections along the first and second dimensions, respectively.
To take full advantage of deep learning, we can stack the above networksfS(x)f_S(x)fS(x) to form a deep neural networkfD(x)f_D(x)fD(x), where the i-th layer is denoted as li(x)=fS(x)l_i(x)=f_S(x)li(x)=fS(x). Therefore, fD(x)f_D(x)fD(x)can be expressed as:
fD(x)=lL∘lL−1∘⋯∘l1∘x,\begin{equation} f_{\text{D}}(x) = l_L \circ l_{L-1} \circ \cdots \circ l_{1} \circ x, \end{equation}fD(x)=lL∘lL−1∘⋯∘l1∘x,
where l1∘xl_1∘xl1∘x indicates that the left function l1l_1l1 acts on the right input xxx,meaning l1(x)l_1 (x)l1(x). However, we found that directly stackingfS(x)f_S (x)fS(x) causes the main parameters of the model fD(x)f_D (x)fD(x) to focus on learning angular frequencies(ωn=2πn/T)(ω_n = 2πn/T)(ωn=2πn/T), and thus ignore the learning of Fourier coefficients (ana_nanandbnb_nbn), as shown below:
fD(x)=lL(lL−1∘lL−2∘⋯∘l1∘x)=BL+WoutL[cos(WinL(l1:L−1∘x)∣∣sin(WinL(l1:L−1∘x))]\begin{align} f_{\text{D}}(x) & = l_L(l_{L-1} \circ l_{L-2} \circ \cdots \circ l_{1} \circ x) \notag \\& = B^L + W^L_\text{out}[\cos(W^L_\text{in} (l_{1:L-1} \circ x)|| \sin(W^L_\text{in}(l_{1:L-1} \circ x))] \end{align}fD(x)=lL(lL−1∘lL−2∘⋯∘l1∘x)=BL+WoutL[cos(WinL(l1:L−1∘x)∣∣sin(WinL(l1:L−1∘x))]
wherel(1:L−1)∘xl_(1:L-1)∘xl(1:L−1)∘x is defined as l(L−1)∘l(L−2)∘…∘l1∘x,WinL(l(1:L−1)∘x)l_(L-1)∘ l_(L-2) ∘… ∘ l_1 ∘ x,W_in^L (l_(1:L-1)∘x)l(L−1)∘l(L−2)∘…∘l1∘x,WinL(l(1:L−1)∘x)for approximating angular frequencies, andWoutLW_{out}^LWoutL is for approximating the Fourier coefficients.
Therefore, the ability of fD(x)f_D (x)fD(x)to approximate the Fourier coefficients is independent of the depth of fD(x)f_D (x)fD(x), which is an undesirable result.
To address this, the research team designed FAN based on the following principles with the below characteristics:
- FAN indicates that the ability of the Fourier coefficients should be positively correlated with their depth;
- The output of any hidden layer can be modeled periodically by subsequent layers using a Fourier series.
The first principle enhances the expressiveness of FAN's periodic modeling by leveraging its depth, while the second ensures that the characteristics of FAN's intermediate layers can be used to perform periodic modeling.
Suppose we decouple fS(x)f_S (x)fS(x) as:
fS(x)=fout∘fin∘x,\begin{equation} f_{\text{S}}(x) = f_{out} \circ f_{in} \circ x, \end{equation}fS(x)=fout∘fin∘x,
wherein
fin(x)=[cos(Winx)∣∣sin(Winx)],fout(x)=B+Woutx.\begin{align} & f_{in}(x) = [\cos(W_\text{in}x)|| \sin(W_\text{in}x)],\\ & f_{out}(x) = B + W_\text{out}x. \end{align}fin(x)=[cos(Winx)∣∣sin(Winx)],fout(x)=B+Woutx.
To meet these two principles, the inputs of FAN's intermediate must use finf_{in}fin and foutf_{out}fout simultaneously, instead of applying them sequentially.
Ultimately, based on this design, FAN's layer φ(x)φ(x)φ(x) is defined as follows:
ϕ(x)≜[cos(Wpx)∣∣sin(Wpx)∣∣σ(Bpˉ+Wpˉx)],\begin{equation} \phi(x) \triangleq [\cos(W_px)|| \sin(W_px)|| \sigma(B_{\bar{p}} + W_{\bar{p}}x)], \end{equation}ϕ(x)≜[cos(Wpx)∣∣sin(Wpx)∣∣σ(Bpˉ+Wpˉx)],
where WpW_pWp ,Wp‾W_{\overline{p}}Wp and Bp‾B_{\overline{p}}Bp are learnable parameters andσσσrepresents the activation function.
The entire FAN is defined as a stack of FAN layer φ(x)φ(x)φ(x):
FAN(x)=ϕL∘ϕL−1∘⋯∘ϕ1∘x,\begin{equation} \text{FAN}(x) = \phi_L \circ \phi_{L-1} \circ \cdots \circ \phi_{1} \circ x, \end{equation}FAN(x)=ϕL∘ϕL−1∘⋯∘ϕ1∘x,
wherein
ϕl(x)={[cos(Wplx)∣∣sin(Wplx)∣∣σ(Bpˉl+Wpˉlx)],if l<L,BL+WLx,if l=L,\begin{equation} \phi_l(x) = \left\{ \begin{array}{ll} [\cos(W^l_px)|| \sin(W^l_px)|| \sigma(B^l_{\bar{p}} + W^l_{\bar{p}}x)], & \text{if } l < L, \\ B^L + W^Lx, & \text{if } l = L, \end{array} \right. \end{equation}ϕl(x)={[cos(Wplx)∣∣sin(Wplx)∣∣σ(Bpˉl+Wpˉlx)],BL+WLx,if l<L,if l=L,
2. FAN performs periodic modeling better than the baseline, with impressive universal performance
- Periodic modeling
The image below shows how FAN and other models perform in periodic modeling. The results showed that existing neural networks (including MLPs, KANs, and transformers) underperformed massively in modeling periodic behavior.
Despite their attempts to approximate these periodic functions, the networks' intrinsic ability limited their performance over a wide range of periodicity. In contrast, FAN delivered far better results than the baseline in all the periodic modeling tasks.
Even more importantly, FAN performed exceptionally well on both in-domain and out-of-domain test data, demonstrating its ability to truly understand the deep principles of periodicity and accurately model it, rather than just "rote" the training data.
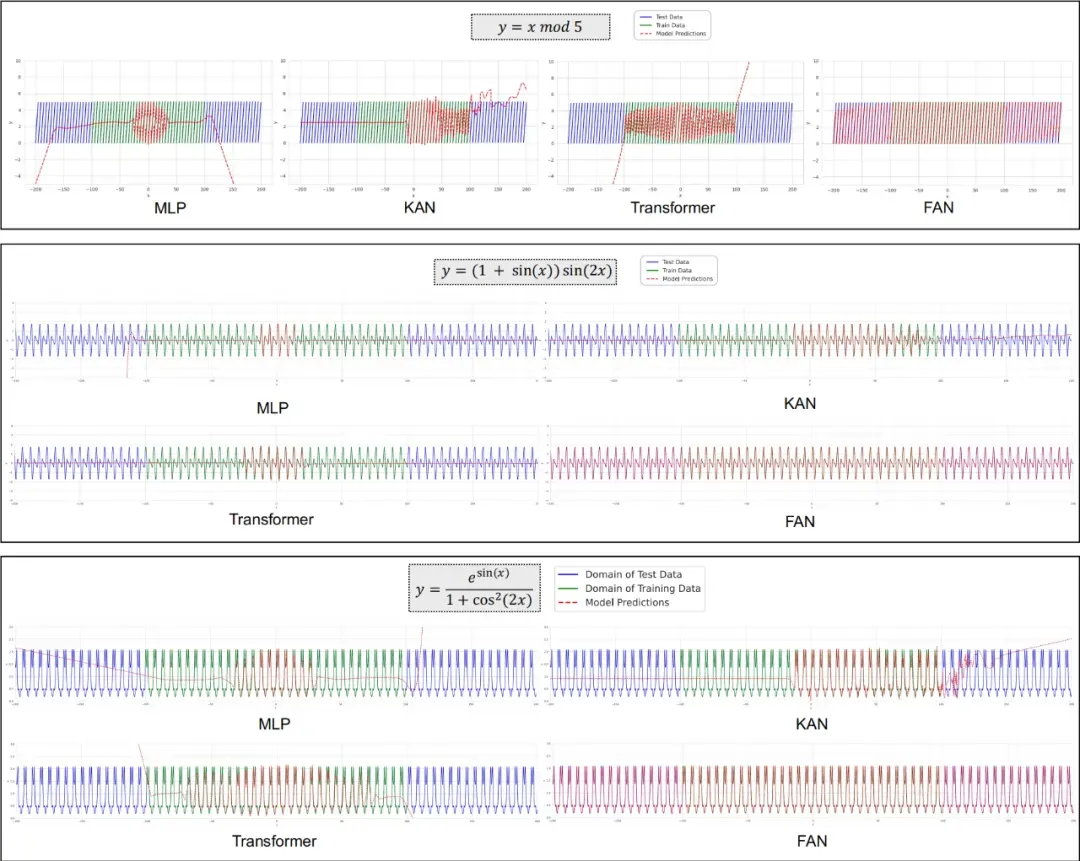
Note: FAN's performance in periodic modeling compared to MLPs, KANs, and transformers. The green and blue lines represent the in-domain and out-of-domain test data of the training data, respectively.
The team also analyzed the training processes of different models in learning complex periodic functions, and included FAN and its variant FAN(Gated), with Gate added in the variant to control the tendency of the FAN layer.
As shown in the graphs below, we can observe 3 conclusions:
- FAN is far superior to other models in terms of convergence speed and final effects.
- Compared to FAN, FAN(Gated) usually achieves faster convergence, but their final performance is still comparable.
- As the number of training rounds increases, even when the training loss of other models stabilizes or gradually decreases, their modeling may differ greatly from the distribution of the test data, resulting in a sharp increase in test loss. This phenomenon further demonstrates the shortcomings of these models in capturing periodicity.
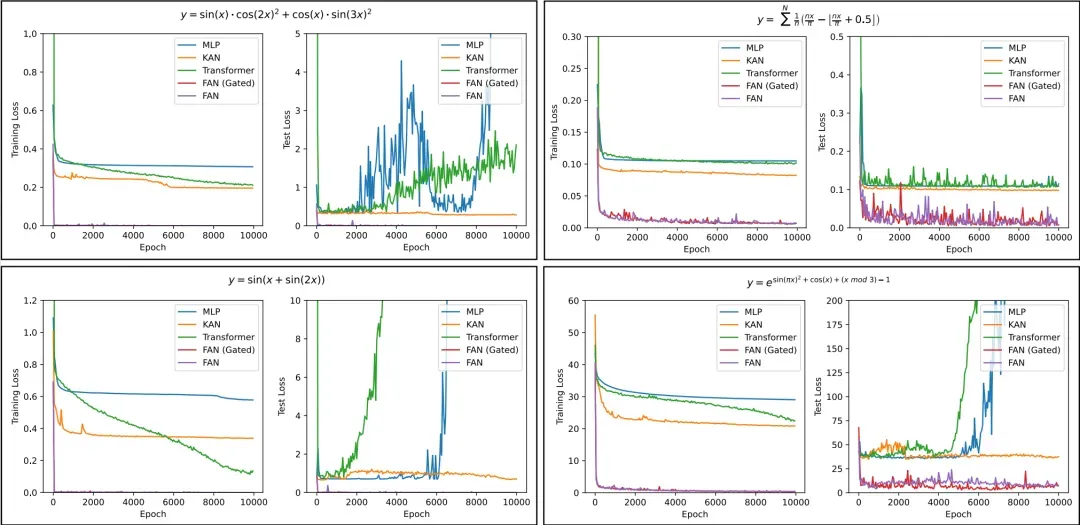
Note: Comparison of training and test losses for different models in the task of learning complex periodic functions
- Symbolic formula representation
From the four common functional expressions applied from different models in mathematics and physics, it can be observed that while KAN is comparable to FAN when the number of parameters is small, its performance drops significantly when the number of parameters increases.
Conversely, as the number of parameters increases, FAN approximates these functions better than other baselines, including MLPs, KANs, and transformers, although many of these functions are only partially periodic or completely aperiodic.
These results showed not only FAN's enhanced ability to model periodicity, but also that its ability to approximate aperiodic function remains intact.
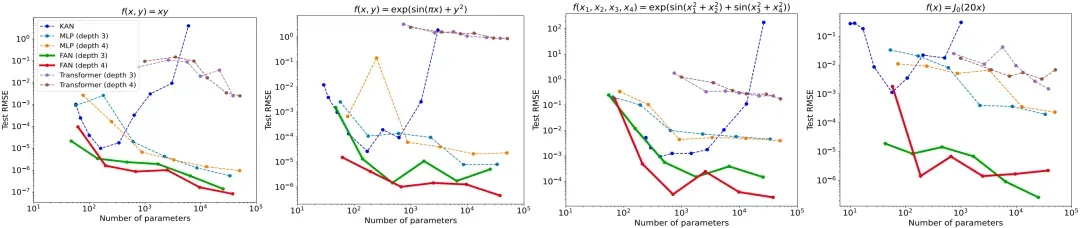
Note: The expressions of params by different models in a task of representing symbolic formulas
- Time series forecasting
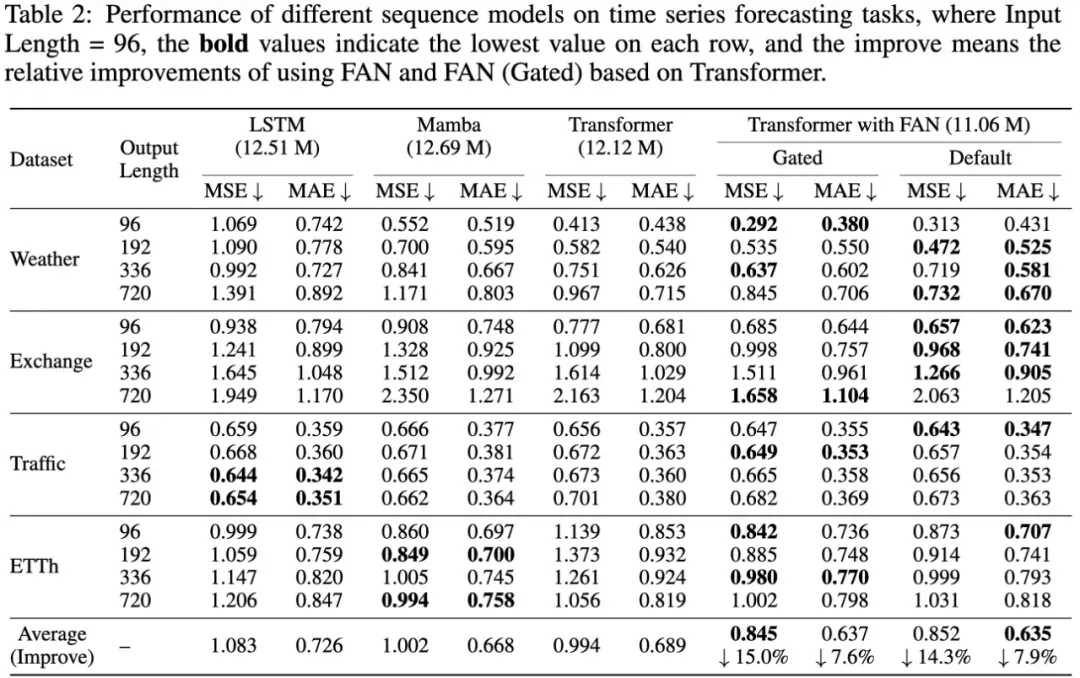
As shown in the table below, the research team compared the performance of transformers with FAN and other sequence models on time series prediction tasks on four public datasets.
In most cases, the transformers with FAN and FAN(Gated) perform the best in these tasks compared to LSTM, Mamba, and standard transformers.
They are a substantial improvement over standard transformers, with average relative improvements of 14.3-15.0% MSE and 7.6-7.9% MAE. These results showed that the inclusion of explicit periodic pattern coding in neural networks can improve time series prediction in real-world applications.
- Language modeling
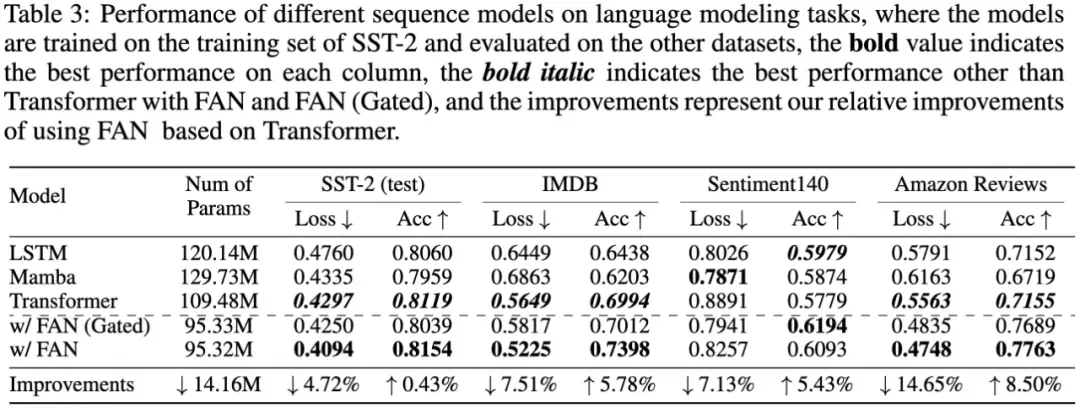
Now, let's look at the performance of different sequence models on four sentiment analysis datasets, as shown in the table below.
It was found that transformers and other sequence models such as LSTM and Mamba combined with FAN and FAN(Gated) performed vastly better, especially in cross-domain zero-shot learning on the datasets of IMDB, Sentiment140 and Amazon Reviews.
Transformers with FAN achieved up to 14.65% and 8.50% relative improvements in loss and accuracy, respectively, while reducing the number of params by about 14.16M. The results demonstrated the potential of periodic modeling to improve effectiveness and generalization in cross-domain language modeling and sentiment analysis tasks.
- Image recognition
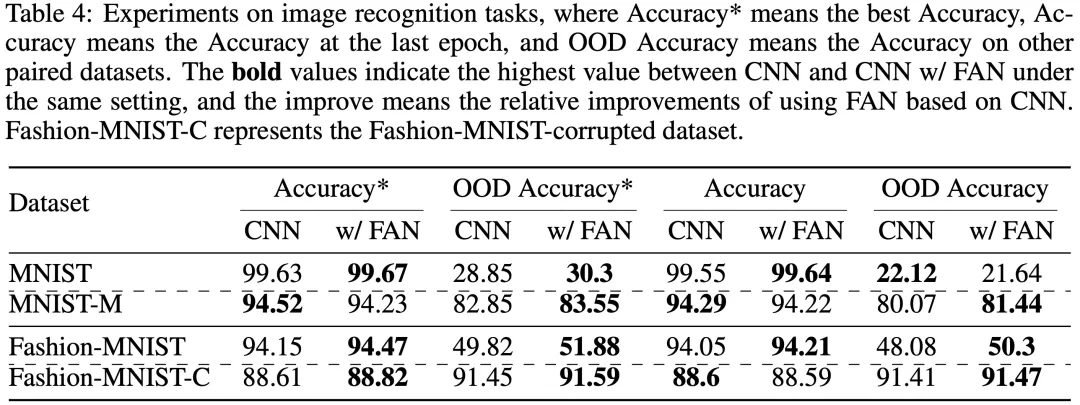
The team also applied FAN to image recognition tasks. On classic MNIST and Fashion-MNIST, the experimental results showed that CNN combined with FAN led in most cases in the optimal accuracy index compared with standard CNN, and also achieved a significant improvement in the OOD accuracy index for optimal out-of-domain detection.
The team was of the view that potential periodic features also exist in image recognition tasks, thus FAN can help CNN perform better to some extent with its ability to model periodic features.
3. FAN is poised to be a strong alternative to MLP
FAN theoretically has the same expressive ability as MLP, because it also follows the universal approximation theorem which ensures its ability to approximate functions. The difference between them is that periodicity is explicitly integrated into FAN, giving it capabilities that traditional MLPs do not possess.
In other words, FAN fully inherits the advantages of MLPs while enhancing the ability to capture data periodicity. Therefore, the team believes that FAN is a promising alternative to MLPs.
Of course, FAN's application is not limited to tasks that explicitly require periodic modeling, as it has also shown strong and broader applicability. In a series of real-world task experiments (such as symbolic formula representation, time series forecasting, and language modeling), the team demonstrated that FAN performed significantly better than MLPs and other baseline models.
In fact, many machine-learning tasks that do not seem to relate directly to periodicity, such as mathematical operations and logical reasoning, may actually have hidden periodicity. At a deeper level, periodicity is not just a data feature, but also a general law or knowledge that allows abstract rules and principles to be transferred and reused between different contexts.
If a neural network lacks the ability to model cyclical features, it may damage its learning efficiency. The team conjectured that this may have something to do with how various past transformer models kept failing to capture cyclical features and generalize them effectively, despite repeated scaling of their parameters and data volumes.
In summary, FAN is expected to be a key component of foundation models, with its enhanced periodic modeling capabilities and reduced params and FLOPS compared to MLP.
In the future, the team plans to expand the application scope of FAN, enhancing its performance as a component of foundation models and continuing to drive its technological progress and innovation. Interested in large-model architectures and exploring cutting-edge topics in the field? Follow the WeChat official account "Doubao (Seed) Team" or tap to read the original article on the official website for more information.