弥补Transformer缺陷,北大字节跳动联合提出FAN,聚焦周期性特征与规律
弥补Transformer缺陷,北大字节跳动联合提出FAN,聚焦周期性特征与规律
日期
2024-11-22
分类
技术发布
近日,北京大学与字节跳动豆包大模型团队联合提出 FAN: Fourier Analysis Networks ,一种新型神经网络架构。
FAN 通过引入傅里叶原理,将周期性信息显式嵌入到网络结构中,使模型更自然地捕捉和理解数据中的周期性特征,并且可用更少参数量和 FLOPs 无缝替换传统 MLP 层。
实验结果表明,FAN 不仅在周期性建模上,表现显著优于现有模型,而且在符号公式表示、时间序列预测、语言建模和图像识别等实际任务中表现出色。面向域外数据,FAN 同样展现出明显优势,这也证明了其对周期规律特征的强大提取与总结能力。
当前,以 Transformer 为基础的大模型已成为主流,典型代表包括 GPT 系列、 Llama 系列 、DiT 架构图像生成模型等等。
然而,集成 MLP 的经典 Transformer 模型在周期性建模方面存在潜在缺陷。即使面对简单的正弦函数,现有 Transformer 模型也难以理解其中周期性规律,在外推时,表现出完全失控状态,未能有效捕捉周期性现象本质。
北京大学李戈教授团队与字节跳动豆包大模型团队近期提出一种新型神经网络架构,FAN(Fourier Analysis Networks)。通过引入傅里叶原理思想,FAN 能够将周期性信息直接嵌入网络结构中,使模型更自然地捕捉和理解数据中的周期性特征。
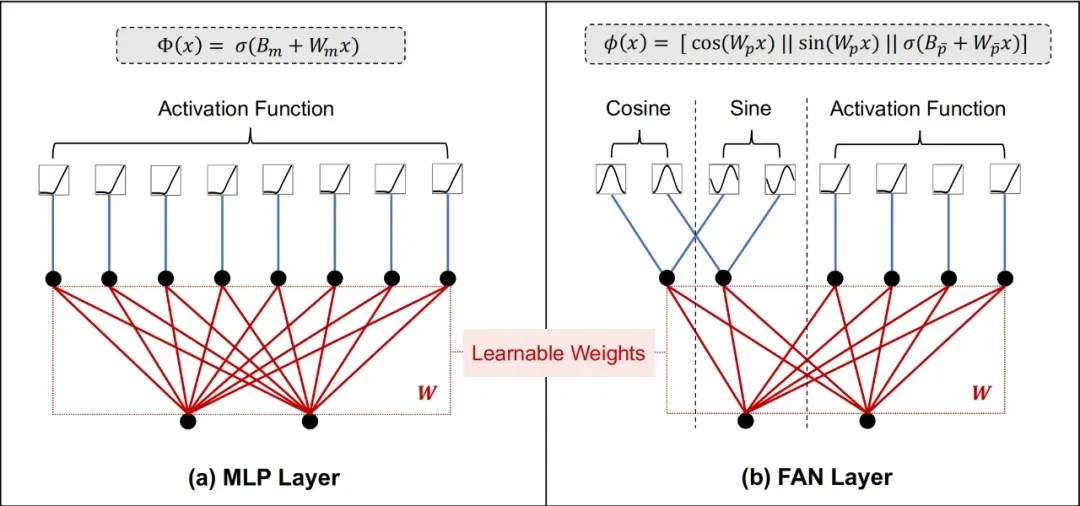
注:MLP Layer 和 FAN Layer 示例
实验表明,FAN 不仅在周期性建模上表现显著优于现有模型,而且在符号公式表示、时间序列预测、语言建模、图像识别等实际任务中,同样表现超过了 Transformer 等主流模型,尤其在域外测试数据上,表现出色。
团队认为,FAN 提供了一种全新范式,可有效地对周期性建模,无缝替换传统 MLP ,同时减少参数量和计算量,填补了当前基础模型在周期性建模方面缺陷,并展示出广泛应用潜力。

FAN: Fourier Analysis Networks
论文链接:https://arxiv.org/abs/2410.02675
1. 在 Transformer 中引入傅里叶原理
周期性现象广泛存在,深刻影响着人类社会和自然科学。作为最重要的基础特性之一,许多规律都显式或隐式地包含周期性,例如天文学中的行星运动、气象学中的季节变化、生物学中的昼夜节律、经济学中的商业周期、物理学中的电磁波以及数学运算和逻辑推理等。
良好的周期性建模可有效提升模型在上述任务表现,然而,现有基础模型严重依赖 case-by-case 式的数据驱动优化方式,缺少明确机制来理解数据中的根本原理。
作为经典数学分析工具,傅里叶级数能将周期函数拆解为一系列简单的正余弦波叠加,广泛应用于信号处理、物理学等领域。研究团队认为,理论上,包含复杂周期特征的数据同样也可以被拆解为简单的正余弦表示。
基于上述思考,北大与豆包大模型联合研究团队希望构建一个简单神经网络来建模傅里叶级数,用以替代 MLP 。
但在实际探索中,团队面临着理论与实践之间的巨大挑战——更改一个基础网络架构,让其在通用任务上性能与 MLP 保持相对一致,本就是一件困难的事,更别说加入全新周期性建模特性并获得提升。尤其神经网络目前仍是“黑箱”,团队同学发现,在实际探索过程中,许多理论上可行的方法,在应用中常常意外失效。
为此,团队尝试了 60 多版修改方案,最终探寻出一个最简洁且高效的方法,也就是 FAN 。

具体来说,团队为构建一个简单的神经网络 fS(x) f_S(x)fS(x) 以表示函数的傅里叶级数展开,我们可以将 fS(x)f_S(x)fS(x) 表示为:
fS(x)≜a0+∑n=1N(ancos(2πnxT)+bnsin(2πnxT)),=(I)a0+∑n=1N(wnccos(wninx)+wnssin(wninx)),=(II)B+[w1c,w2c,⋯ ,wnc]cos([w1in∣∣w2in∣∣⋯∣∣wnin]x)+[w1s,w2s,⋯ ,wns]sin([w1in∣∣w2in∣∣⋯∣∣wnin]x)=B+Wccos(Winx)+Wssin(Winx),=(III)B+Wout[cos(Winx)∣∣sin(Winx)],\begin{equation} \begin{aligned} f_{\text{S}}(x) & \triangleq a_0 + \sum_{n=1}^{N} \left( a_n \cos\left(\frac{2\pi nx}{T}\right) + b_n \sin\left(\frac{2\pi nx}{T}\right) \right), \\ & \mathop{=}\limits^{(\text{I})} a_0 + \sum_{n=1}^{N} \left( w^c_n \cos\left(w^\text{in}_nx\right) + w^s_n \sin\left(w^\text{in}_nx\right) \right), \\ & \mathop{=}\limits^{(\text{II})} B + [w^c_1, w^c_2, \cdots, w^c_n] \cos([w^\text{in}_1|| w^\text{in}_2|| \cdots|| w^\text{in}_n] x) \\ & \quad + [w^s_1, w^s_2, \cdots, w^s_n] \sin([w^\text{in}_1|| w^\text{in}_2|| \cdots|| w^\text{in}_n] x) \\ & = B + W_c \cos(W_\text{in}x) + W_s \sin(W_\text{in}x), \\ & \mathop{=}\limits^{(\text{III})} B + W_\text{out}[\cos(W_\text{in}x)|| \sin(W_\text{in}x)], \end{aligned} \end{equation}fS(x)≜a0+n=1∑N(ancos(T2πnx)+bnsin(T2πnx)),=(I)a0+n=1∑N(wnccos(wninx)+wnssin(wninx)),=(II)B+[w1c,w2c,⋯,wnc]cos([w1in∣∣w2in∣∣⋯∣∣wnin]x)+[w1s,w2s,⋯,wns]sin([w1in∣∣w2in∣∣⋯∣∣wnin]x)=B+Wccos(Winx)+Wssin(Winx),=(III)B+Wout[cos(Winx)∣∣sin(Winx)],
其中,B、WinW_{in}Win、WoutW_{out}Wout 为可学习参数,(I) 根据 ana_nan 和 bnb_nbn 通过定积分计算,(II) 和 (III) 是矩阵运算的等价形式,[・||・] 和 [・,・] 分别表示沿第一维度和第二维度的连接。
为了充分利用深度学习优势,我们可以堆叠上述网络 fS(x)f_S(x)fS(x) 形成深度神经网络 fD(x)f_D(x)fD(x) ,其中第 i 层表示为 li(x)=fS(x)l_i(x)=f_S(x)li(x)=fS(x) 。因此,fD(x)f_D(x)fD(x) 可以表示为:
fD(x)=lL∘lL−1∘⋯∘l1∘x,\begin{equation} f_{\text{D}}(x) = l_L \circ l_{L-1} \circ \cdots \circ l_{1} \circ x, \end{equation}fD(x)=lL∘lL−1∘⋯∘l1∘x,
其中,l1∘xl_1∘xl1∘x 表示左侧函数 l1l_1l1 作用于右侧输入 xxx ,即 l1(x)l_1 (x)l1(x) 。然而,我们发现直接堆叠 fS(x)f_S (x)fS(x) 会导致模型 fD(x)f_D (x)fD(x) 的主要参数集中于学习角频率 (ωn=2πn/T)(ω_n = 2πn/T)(ωn=2πn/T) ,从而忽略了傅里叶系数 (ana_nan和bnb_nbn) 的学习,如下所示:
fD(x)=lL(lL−1∘lL−2∘⋯∘l1∘x)=BL+WoutL[cos(WinL(l1:L−1∘x)∣∣sin(WinL(l1:L−1∘x))]\begin{align} f_{\text{D}}(x) & = l_L(l_{L-1} \circ l_{L-2} \circ \cdots \circ l_{1} \circ x) \notag \\& = B^L + W^L_\text{out}[\cos(W^L_\text{in} (l_{1:L-1} \circ x)|| \sin(W^L_\text{in}(l_{1:L-1} \circ x))] \end{align}fD(x)=lL(lL−1∘lL−2∘⋯∘l1∘x)=BL+WoutL[cos(WinL(l1:L−1∘x)∣∣sin(WinL(l1:L−1∘x))]
其中,l(1:L−1)∘xl_(1:L-1)∘xl(1:L−1)∘x 定义为 l(L−1)∘l(L−2)∘…∘l1∘xl_(L-1)∘ l_(L-2) ∘… ∘ l_1 ∘ xl(L−1)∘l(L−2)∘…∘l1∘x,WinL(l(1:L−1)∘x)W_in^L (l_(1:L-1)∘x)WinL(l(1:L−1)∘x) 用于近似角频率,WoutLW_{out}^LWoutL 用于近似傅里叶系数。
因此,fD(x)f_D (x)fD(x) 拟合傅里叶系数的能力与 fD(x)f_D (x)fD(x) 的深度无关,这是一个不理想的结果。
为了应对这一问题,研究团队根据以下原则设计了 FAN ,它具备以下特性:
- FAN 表示傅里叶系数的能力应与其深度正相关;
- 任何隐藏层的输出都可以通过后续层使用傅里叶级数来建模周期性。
第一个原则通过利用 FAN 的深度增强了其周期性建模的表现力,而第二个原则确保 FAN 中间层的特征可用于执行周期性建模。
假设我们将 fS(x)f_S (x)fS(x) 解耦为:
fS(x)=fout∘fin∘x,\begin{equation} f_{\text{S}}(x) = f_{out} \circ f_{in} \circ x, \end{equation}fS(x)=fout∘fin∘x,
其中
fin(x)=[cos(Winx)∣∣sin(Winx)],fout(x)=B+Woutx.\begin{align} & f_{in}(x) = [\cos(W_\text{in}x)|| \sin(W_\text{in}x)],\\ & f_{out}(x) = B + W_\text{out}x. \end{align}fin(x)=[cos(Winx)∣∣sin(Winx)],fout(x)=B+Woutx.
为了满足这两个原则,FAN 的中间层输入需要同时使用 finf_{in}fin 和 foutf_{out}fout 而不是依次应用它们。
最终,FAN 基于此设计,其 FAN 层 φ(x)φ(x)φ(x) 定义如下:
ϕ(x)≜[cos(Wpx)∣∣sin(Wpx)∣∣σ(Bpˉ+Wpˉx)],\begin{equation} \phi(x) \triangleq [\cos(W_px)|| \sin(W_px)|| \sigma(B_{\bar{p}} + W_{\bar{p}}x)], \end{equation}ϕ(x)≜[cos(Wpx)∣∣sin(Wpx)∣∣σ(Bpˉ+Wpˉx)],
其中 WpW_pWp 、Wp‾W_{\overline{p}}Wp、Bp‾B_{\overline{p}}Bp 是可学习参数,σσσ 表示激活函数。
整个 FAN 定义为 FAN Layer φ(x)φ(x)φ(x) 的堆叠:
FAN(x)=ϕL∘ϕL−1∘⋯∘ϕ1∘x,\begin{equation} \text{FAN}(x) = \phi_L \circ \phi_{L-1} \circ \cdots \circ \phi_{1} \circ x, \end{equation}FAN(x)=ϕL∘ϕL−1∘⋯∘ϕ1∘x,
其中
ϕl(x)={[cos(Wplx)∣∣sin(Wplx)∣∣σ(Bpˉl+Wpˉlx)],if l<L,BL+WLx,if l=L,\begin{equation} \phi_l(x) = \left\{ \begin{array}{ll} [\cos(W^l_px)|| \sin(W^l_px)|| \sigma(B^l_{\bar{p}} + W^l_{\bar{p}}x)], & \text{if } l < L, \\ B^L + W^Lx, & \text{if } l = L, \end{array} \right. \end{equation}ϕl(x)={[cos(Wplx)∣∣sin(Wplx)∣∣σ(Bpˉl+Wpˉlx)],BL+WLx,if l<L,if l=L,
2. FAN 的周期建模能力显著优于基线,通用性能亦有不错表现
- 周期建模
下方图片展示了 FAN 和其他模型在周期性建模中的表现。结果表明,现有神经网络(包括 MLP 、KAN 和 Transformers )在建模周期性方面表现明显不足。
尽管它们试图拟合这些周期函数,然而,内在能力限制了它们在大范围周期性上的性能表现。相比之下,FAN 在所有这些周期性建模任务中,都明显优于基线。
更值得一提的是,FAN 在训练数据域内和域外测试数据上都表现得非常出色,表明它能够真正理解周期性的深刻原理,并对其进行精准建模,而不仅仅是“死记硬背”训练数据。
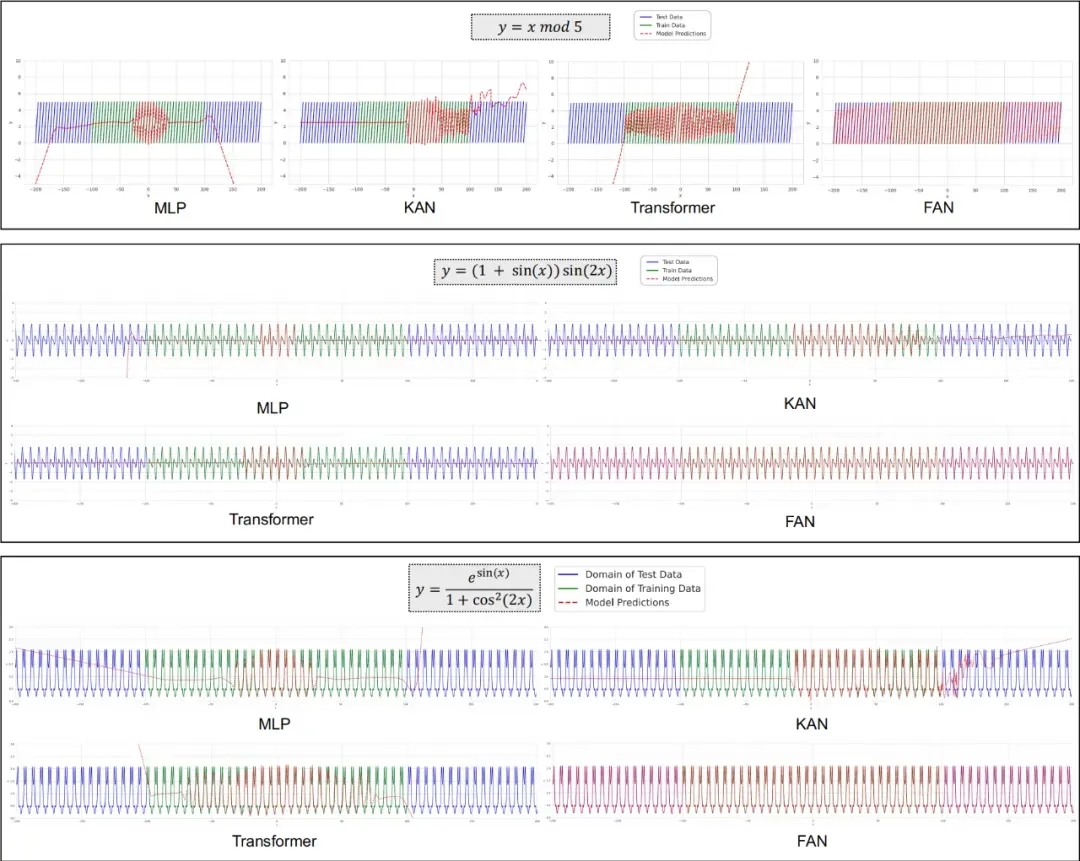
注:FAN 在周期性建模中的表现与 MLP 、KAN 和 Transformer 相比,其中绿线表示训练数据域内测试数据,而蓝线表示训练数据域外测试数据。
研究团队还分析了不同模型在学习复杂周期函数任务上的训练过程,并加入了 FAN 及其变体 FAN(Gated) ,在该变体中,团队添加了 Gate 来控制 FAN Layer 的倾向。
如下图所示,我们能观察到 3 个结论:
1)FAN 在收敛速度和最终效果方面都远远超过其他模型。
2)与 FAN 相比,FAN(Gated) 通常可以实现更快收敛,但最终性能仍然相当。
3)随着训练轮数增加,虽然其他模型的训练损失变得稳定或逐渐减少,但它们的建模可能与测试数据分布有很大差异,导致测试损失急剧增加。这一现象进一步证明了这些模型在捕捉周期性方面的缺陷。
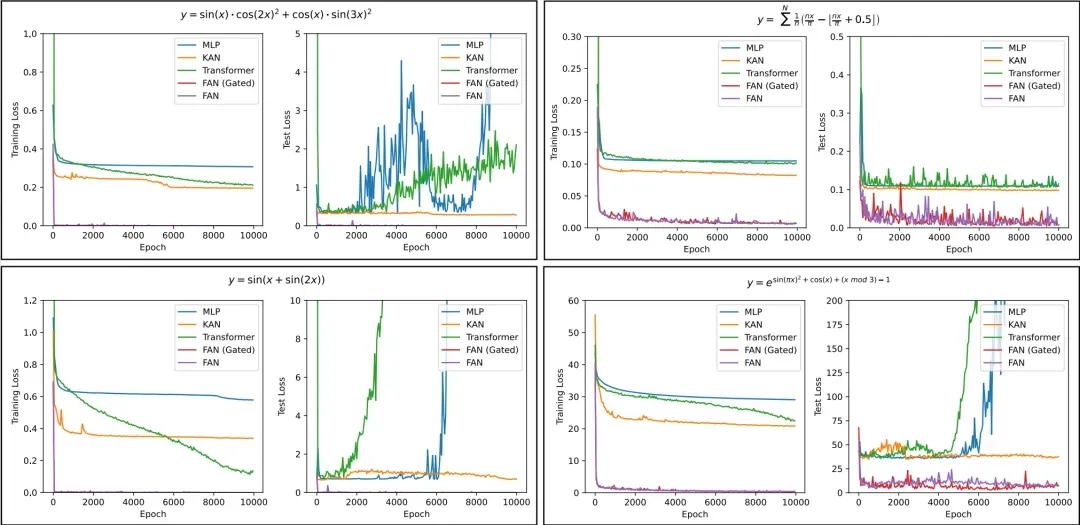
注:不同模型在学习复杂周期函数任务上的训练和测试损失比较
- 符号公式表示
从不同模型应用于数学和物理学中的四个常见函数表现,可以观察到,虽然 KAN 在参数数量较少时,能与 FAN 相媲美,但随着参数数量增加,其性能会显著下降。
相反,随着参数数量增加,FAN 拟合这些函数始终优于其他基线,包括 MLP 、KAN 和 Transformer ,尽管这些函数中,许多只是部分周期性或完全非周期性的。
这些结果表明,FAN 不仅增强了对周期性的建模能力,同时也没有损害拟合非周期性函数的能力。
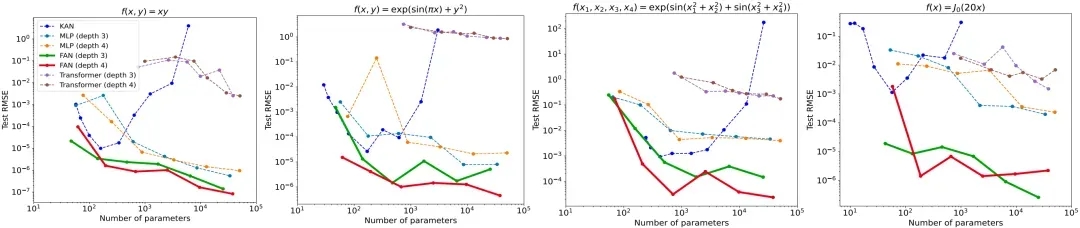
注:不同模型在符号公式表示任务中不同参数量的表现
- 时间序列预测
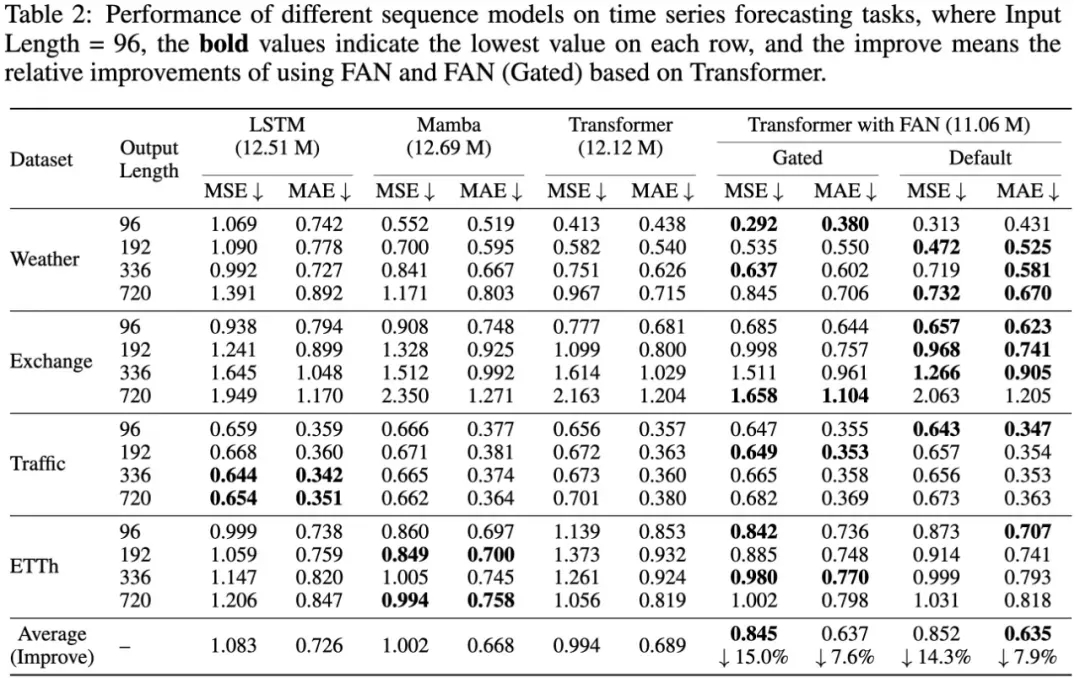
如下表所示,研究团队在四个公共数据集上比较了结合 FAN 的 Transformer 和其他序列模型在时间序列预测任务上的表现。
在大多数情况下,与 LSTM 、 Mamba 和标准的 Transformer 相比,结合 FAN 和 FAN(Gated) 的 Transformer 在这些任务上取得了最佳性能。
它们相对于标准 Transformer 改进显著。平均相对改进范围为 14.3%-15.0% 的 MSE 和 7.6%-7.9% 的 MAE 。这些结果表明,在神经网络中加入显式周期模式编码可以提高实际应用中的时间序列预测性能。
- 语言建模
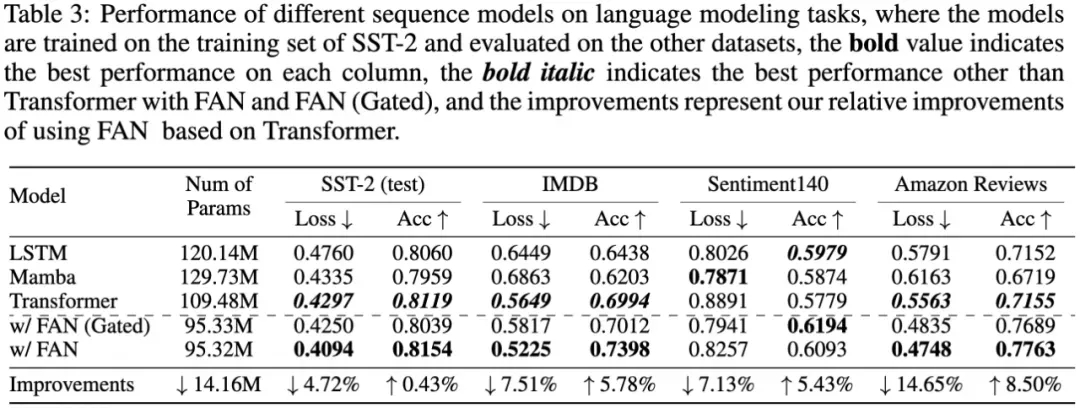
再看不同序列模型在四种情绪分析数据集上的性能比较,如下方表格所示。
可以发现,结合 FAN 和 FAN(Gated) 的 Transformer 与标准 Transformer 和其他序列模型,例如 LSTM 和 Mamba,表现出明显的优越性能,尤其是在 IMDB 、Sentiment140 和 Amazon Reviewers 数据集上的零样本跨领域表现突出。
结合 FAN 的 Transformer 在损失和准确度方面分别实现了最高 14.65% 和 8.50% 相对改进,同时,将参数数量减少了约 14.16M 。结果表明,周期性建模在跨领域语言建模和情绪分析任务上,具有提高有效性和泛化潜力。
- 图像识别
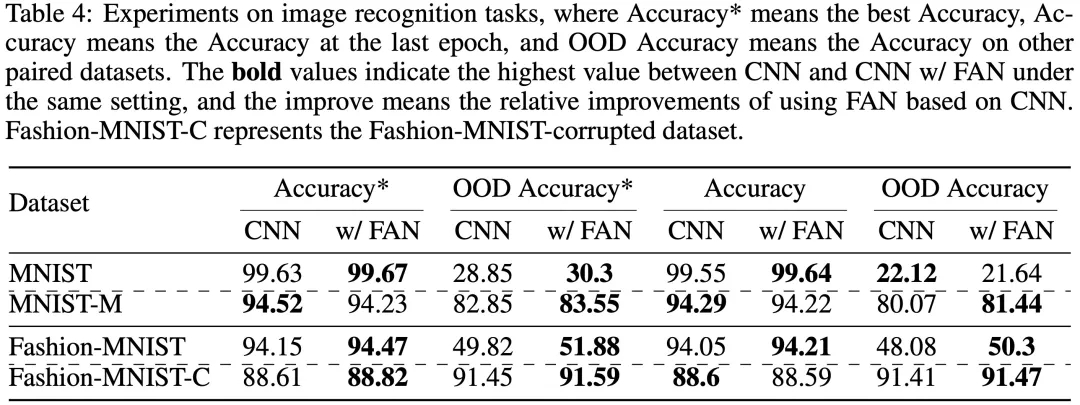
团队还将 FAN 应用到了图像识别任务上。在经典 MNIST 和 Fashion-MNIST 上,实验结果表明,结合 FAN 的 CNN 与标准 CNN 相比,在最优 Accuracy 指标上取得了大多数情况下的领先,而在最优域外检测 OOD Accuracy 指标上,也取得了较明显提升。
团队认为,图像识别任务中也存在潜在的周期性特征,FAN 建模周期性特征能力可以一定程度上辅助 CNN 获得更优表现。
3. FAN 有望成为 MLP 的有力替代
FAN 在理论上具有与 MLP 相同的表达能力,因其同样遵循通用近似定理,确保了其函数近似能力。不同的是,FAN 明确纳入周期性,使其具备传统 MLP 所不具备的能力。
换而言之,FAN 全面继承了 MLP 既有优势,还增强了捕获数据周期性特征的能力。因此,团队认为 FAN 有望作为 MLP 的有力替代。
当然,FAN 的落地空间不仅限于明确需要周期性建模的任务,在更广泛应用中, FAN 也展现出强大的适用性。研究团队通过一系列现实世界任务实验(如符号公式表示、时间序列预测和语言建模等)证明,FAN 的表现明显优于 MLP 和其他基线模型。
事实上,许多看似与周期性无直接关联的机器学习任务,如数学运算和逻辑推理,实际上也可能隐藏着周期性。从更深层次来看,周期性不仅仅是一种数据特征,还反映了一种更为普遍的规律或知识,即允许抽象的规则和原理在不同上下文之间转移和重用。
倘若神经网络缺乏对周期性特征的建模能力,则可能会损害其学习效率,团队由此推测,过往基于 Transformer 的诸多模型参数及数据量一再 Scaling ,仍对规律性特征总结不佳、泛化能力不强,或与此相关。
总结来看,FAN 与 MLP 相比,不仅增强了周期性建模能力,且参数量和计算量更少,有望成为基础模型的关键组成部分。
未来,团队计划进一步扩大 FAN 的应用范围,增强其作为基础模型组件的表现,持续推动基础模型技术进步与创新发展。如果你也对大模型基础架构工作感兴趣,有志于探索前沿课题,欢迎前往招聘页面,了解岗位详情。